Lurking in the interwebs and Markov chains

It's procrastination time once again. I open up the web browser and start going around, "surfing" the web, clicking on links and doing such things. But how does my mind work? How do I click the next link. The pointless browsing around in the web, is an experience I feel we all can feel close to. Many scientists have tried to find patterns in such behaviors, to find models that describe them, probably in order for business-people to sell us more gadgets, but alas, I digress.

The point is I feel that in our most insignificant moments, the moments where are choices are not inherently rational, is a point of behavior we people struggle to recognize and most importantly to anticipate. Science has done great work to research such issues. For this post, I'll be considered with one simple question. When mindlessly browsing around, how far (in our browsing history) can we track the the influence to our next choice of link? In particular when choosing a link, does it matter where I am, where I was two links before, three links before, or is it maybe completely random.

Trying to answer the previous question I will try to present and recreate, at least partially, the paper by Singer, Helic, Taraghi and Strohamier, "Detecting Memory and Structure in Human Navigation Patterns Using Markov Chain Models of Varying Order". Here there is provided a model with which we can simulate the hypotheses of our problem, and test them on some public data.

To make the methodology clear, first we have to talk a bit about Markov chains. They are a model (stochastic model), that describes the sequence of events. In these chains, the probability to for an event to arise depends only on the state of a number of past events. Here we will use a discrete time Markov chain since the interactions with a website happen in discrete time, i.e. every time the user hits on a new link.

The order of Markov chain is the number of events we have to take in mind when calculating the probability for a next event. For example for an order of 2 we have to take in mind two events in the past. For the readers that have some background in probability notations that would mean that: \[ P(X_{n+1}) = x_{n+1} \vert X_1 = x_1, X_2 = x_2, \ldots, X_n = x_n) = P(X_{n+1} = x_{n+1} \vert X_{n-1} = x_{n-1}, X_n = x_n )\],

with \(X_i\) being the random variable which models the i-th event.

Just a long equation to show that the probability of the next event just depends, on the two events that preceded it.

In our case, we want to see whether the way we choose the next topic to browse in a web page can be modeled by a higher-order Markov chain. Most applications assume that human navigation is memory-less i.e. just the page we our currently browsing affects our next link. Together with the fact that higher-order models are more complex, this has proved out to be fairly pragmatic with applications that include google's pagerank algorithm. However a deeper understanding of the relation of our choices in navigation can provide deeper insight for the way we use computers (or computers use us, but let's leave these comments for the epilogue).

To test our cases we will use some the following method:

1. Fit the data into Markov chains of order up to 5
2. Compare the models using the likelihood ratio and the AIC, BIC criteria.

I tried to recreate the tools that where developed for the aforementioned paper in R¹. In hindsight R was not the most appropriate language for this (or I was not the most suitable person to develop them in R) but at least it was working. Anyways my implementation in R, along with a sloppy Common Lisp implementation can be found here.

For demonstration we will use the famous MSNBC dataset², which provides paths of topical navigation, i.e. navigation nodes between topics. To prepare the data we add another topic as filler between the distinct paths, so we can treat the dataset as one ergodic Markov Chain. The number of filler topic nodes is relevant to the order of Markov chain we want to fit as.

The frequencies of the topics in our dataset can be seen below:

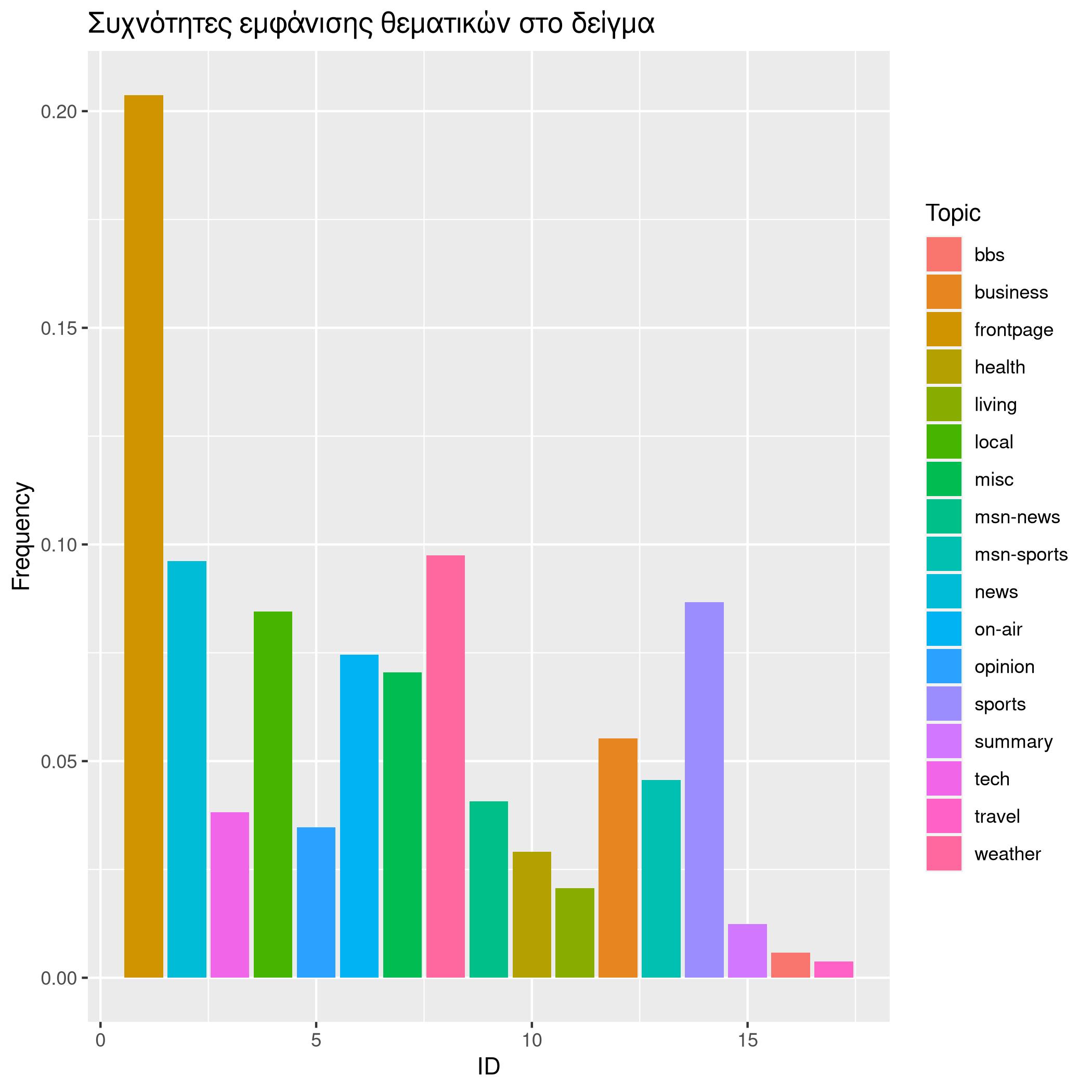
Running:

simulation("dataset", max-order, number-of-states)

we get the following results: Graphing these results we can get more insight one them:

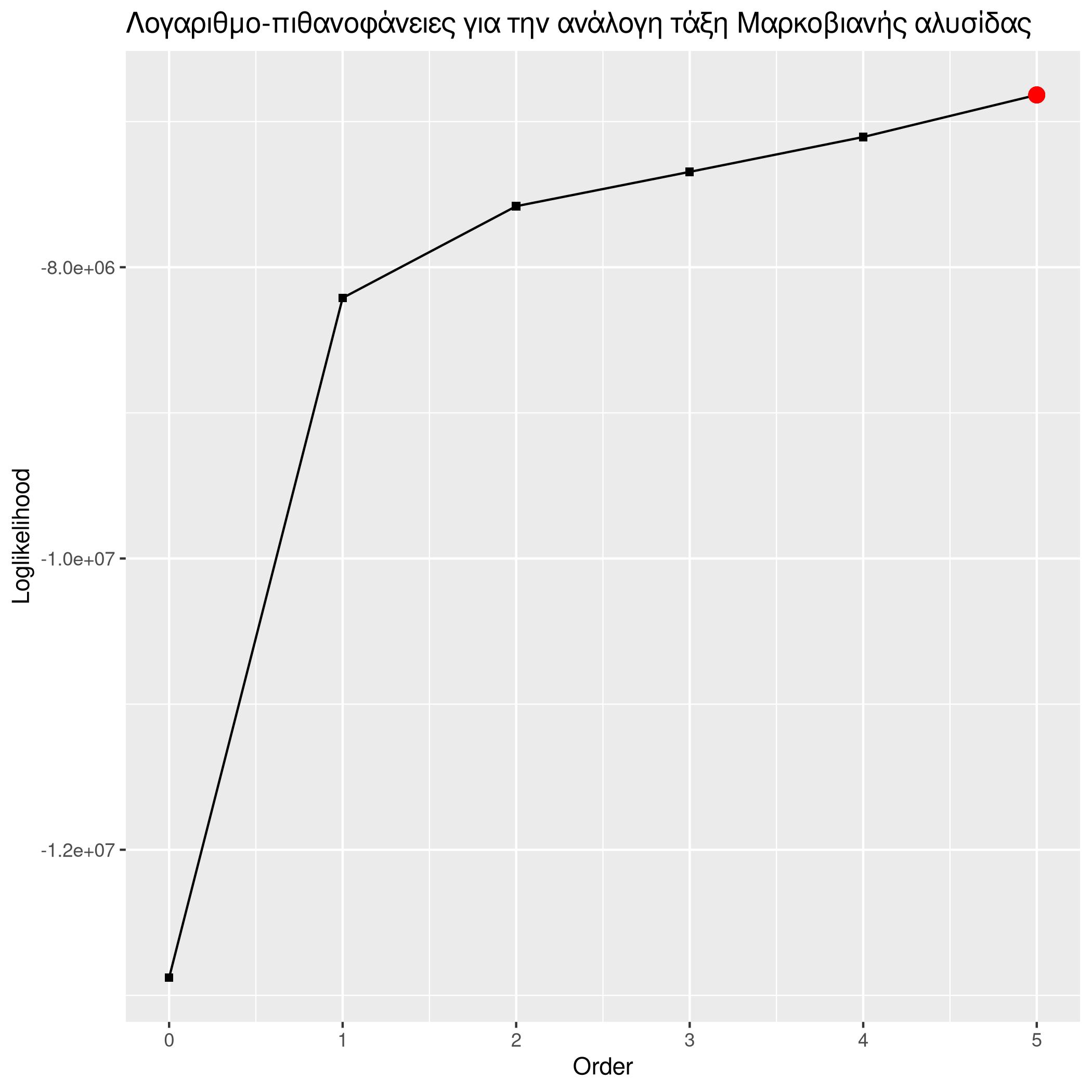
The log-likelihoods seem to always suggest higher-order models. This is to be expected since, high-order models are encapsulating the lower-order ones. To bypass this we can use the likelihood-ratio and do hypothesis testing between each two models. Still observing the previous data we can see that going from order one models to higher the p-value is also and as such we have a very small significance level, which makes us to prefer higher order models.

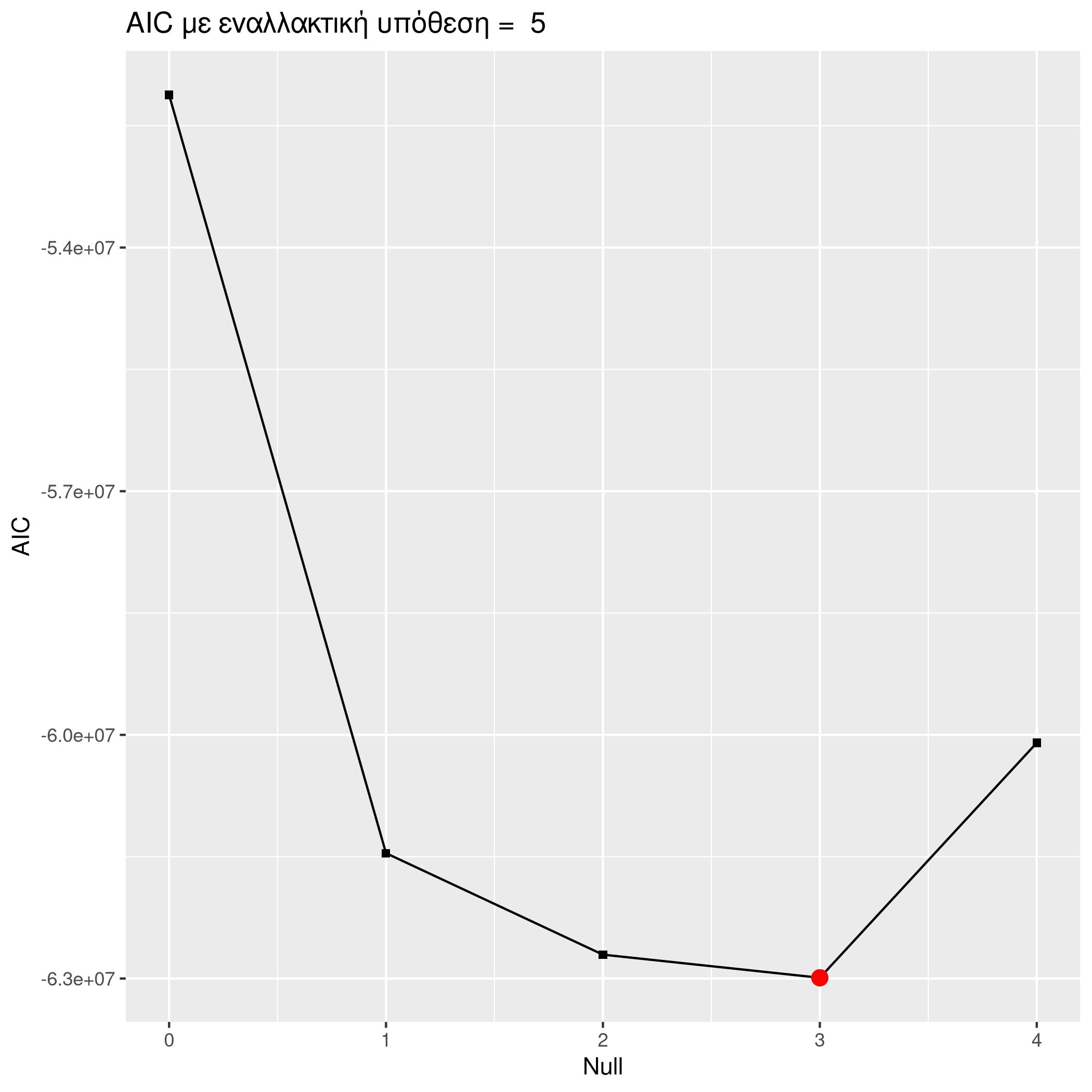
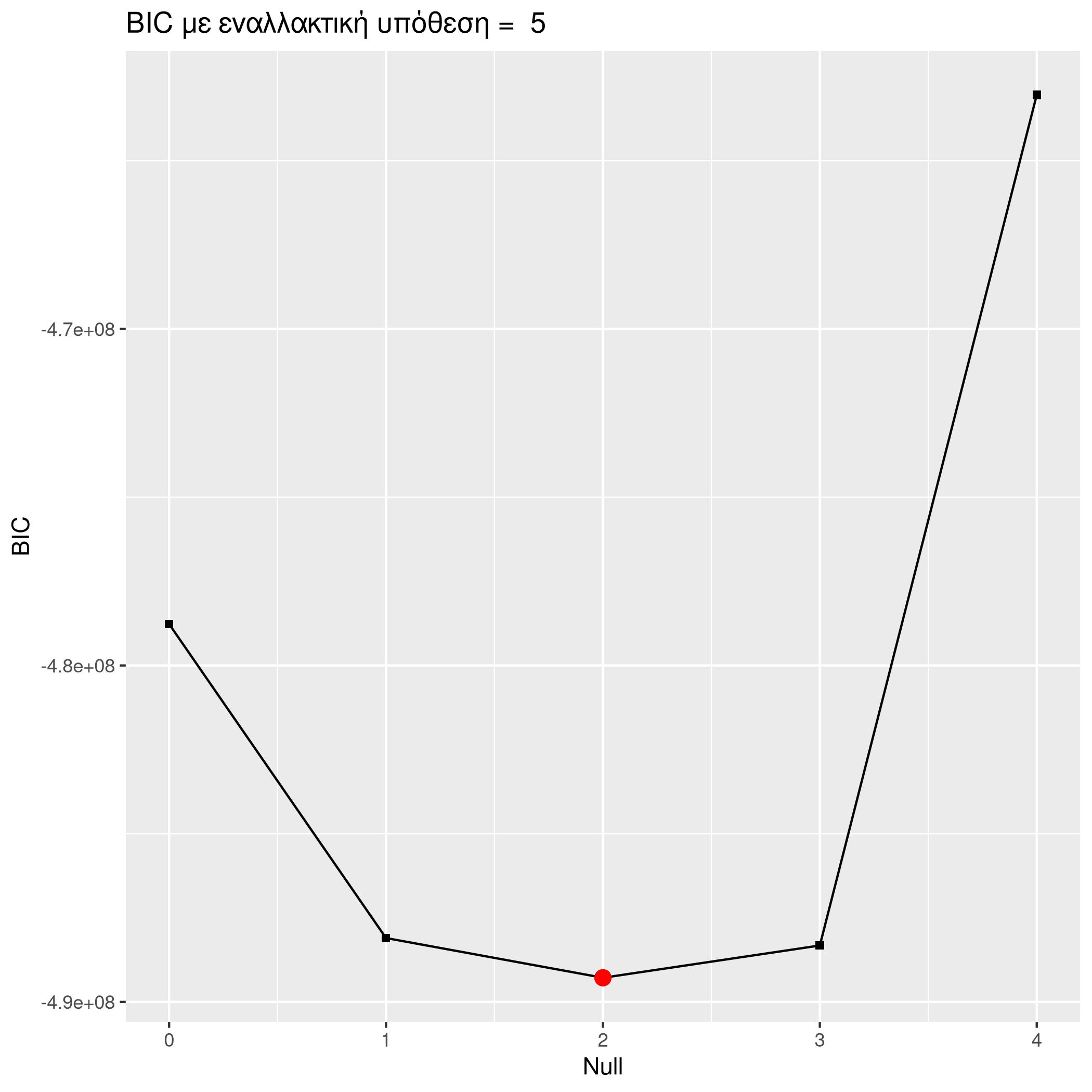
The AIC and BIC criteria seem to suggest the second and third order models accordingly.

So, is it worth it, to create algorithms that are based on higher order models? The data (presented here but most importantly in the paper presented at the start) seem to suggest that this is the case. However our world is one of concessions. Higher order Markov chains induce a high complexity in algorithms, with non researched margins of improvement. At the same time, they could be a very probable step forward in suggestion algorithms and such problems. Time only will tell!